Pattern formation within a segment: dynamic regulation of a neighbourhood of structures
A widespread pattern in biology is segmentation. The body segments of insects or the segments of insect legs are examples. They are clearly a repetitive pattern but, as the rule, the segments are different from each other. Segments have an internal polarity, frequently visible by overt structures such as bristles or spines. The pattern within a segment is recognizable by characteristic landmarks. The pattern of the tobacco hornworm Manduca is an instructive example. The dorsoventral position of the black and the white marks depends in a systematic manner on their AP-position within the segment. In other words, each region must know its position within the segment. The black spots are restricted to a particular AP position.

Information about how the pattern within a segment is regulated has been obtained from surgical interference in hemimetabolous insects (i.e., insects that have from beginning an appearance similar to the adults but no larval stages). Creating a discontinuity in the normal neighborhood of structures by grafting a piece of the cuticula together with the underlying ectoderm to a different position within the segment provokes pattern regulation [1,2]. After one or two moults, a new stable pattern becomes established. The result of such regulation is a restoration of the normal neighborhood of structures; the discontinuity disappears. However, the resulting pattern can be dramatically different from the natural pattern. The figure below shows as an example a transplantation experiment with cockroach legs [3].
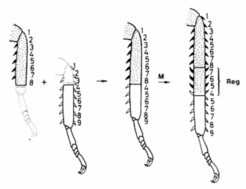
If we denote the normal sequence of structures within a segment as 123...9, a combination of a stump 12345678 and a grafted piece 456789 leads after the mould (M) to the structure 12345678765456789. Although the leg was already too long after the operation, even more structures became inserted by intercalary regeneration (written in bold face, Reg in the figure). After this intercalation, each structure has a neighbor that would be also a neighbor in the non-perturbed situation. Obviously, it is not the natural sequence of elements but the normal neighborhood that is regulated. This argues against mechanisms according to which a segment is organized by a gradient generated by a source at one segment border and a sink at the other since, after a manipulation as described above, a restoration of the normal monotonic sequence would be expected. As indicated by the reversed orientation of the spines, the surplus structures are intercalated with a reversed polarity. Thus, the polarity of the pattern within a segment results from the sequence of elements and not from the alignment of polar cells since a reversal cell polarity occur without any rotation of a part.
Mutual activation of cell states that locally exclude each other
The possibility to generate a sequence of structures by gene activation under the influence of a gradient has been outlined above (see gene activation ). In such a mechanism, the cells do not communicate directly with each other to obtain the correct determination. They measure the local concentration of a substance and behave accordingly. Due to this lack of communication, as a rule, a discontinuity cannot be repaired; especially when at later stages the signaling gradient is no longer available. The cells maintain the once obtained state of determination. A gradient mechanism is therefore inconvenient to account for a dynamic regulation of a correct neighborhood.
However, if two or more such cell states not only exclude each other locally but activate each other mutually over longer ranges, these cell states stabilize each other in a symbiotic manner. Neighboring cell states need each other close by while the local exclusion assures that these states do not merge or overlap (Meinhardt and Gierer, 1980 ). The most stable state is reached if a region in which a particular gene is active is bordered by regions in which the genes for the correct neighboring structures are active. According to this model, segmentation requires the following molecular ingredients:
- Genes (or more general feedback loops) must exist that have a positive feedback on their own activation.
- These activities are locally exclusive; only one of the alternative genes can be active in a given cell.
- Long ranging molecules provide a mutual activation of those cell states that eventually become neighbors. Each cell state in a given cell depends on the help from different cell states in neighboring regions.
The theoretical prediction found meanwhile direct support:. In Drosophila the gene engrailed (en) is a key gene for segmentation. It has a direct autocatalytic feedback on its own activation. Likewise, the specification of the anterior compartment is based on an autocrine feedback loop employing wingless (wg), sloppy paired (slp) and other components. The cell states depend on each other through reciprocal signaling:
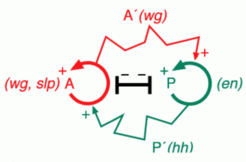
The wg signal is necessary to maintain the autoregulation of en in posterior cells while the hedgehog (hh) signal produced under en control upregulates cubitus interruptus (ci) in anterior cells, a gene that, in turn, activates wg. The repression of ci by en in the posterior compartment results in the suppression of wg at that location. By theoretical explorations of more complex genetic networks, von Dassow et. al. [4] found a direct positive feedback loop for engrailed to be indispensable for a correct segmentation of Drosophila, confirming our minimum model. (For further references see [4,5]). The prediction of such a complex molecular interaction by a theory could hardly be more precise.
The following simulations show the dynamic behaviour of two such locally competing feedback loops that activate each other on long range. Minor asymmetries are able to initiate pattern formation (left simulation below). Since both loops have equal rights, there is no longer an activated and a non-activated region. The system has the capability of size regulation.
Partial removal of a region in which one loop is active (red) leads to pattern regulation with the expansion of the region that is to small on the expense of the larger one:
This size regulation works only if elements of the autocatalytic loops can be exchanged between cells. If this is not the case, the border between two specification cannot be shifted. The progeny of a cell will maintain a once obtained specification, i.e., cells obey a lineage restriction and the border between two such specifications act as compartment border. This is situation in insects since the transcription factor engrailed is restricted to the nucleus and cannot exchanged between the cells.
If one of the competing loops (for instance, engrailed) becomes non-functional due to a mutation, the second loop will become extinct too (right) although there is no longer a competitor present. However, there is also no longer the obligatory support from the other cell state by the diffusible co-factor such as hedgehog.
It is a feature of these interactions that they can generate stripes. A stripe-like gene activation causes long borders between the regions. A particular cell type is close to the cell types that are required for stabilization. This facilitates the mutual support by the diffusible substances. A stripe-like arrangement is therefore especially stable. Many genes involved in the segmentation of Drosophila are expressed in narrow stripes.
The same reaction can act as oscillator. Together with the pattern forming capability its allows a sequential conversion of a periodic pattern in time into a periodic pattern in space. This plays a decisive role in somite formation .
Segmentation: the repetitive pattern of (at least) three cell states
The simplest periodic structure would consist of an alternation of two cell states, let us say, A and P. The two compartments found in Drosophila appear to support such a view. However, such a binary sequence has no polarity, in contrast to the biological observation. No signal would be available that indicates at which AP-border will form the segment border; the grouping could be AP/AP/AP or ..A/PA/PA/P.. Both sequences would have opposite polarity. This problem has two possible solutions:
(i) an additional pattern with a repeat length of two segments exists, consisting for instance of a pattern ..OEOE..; O and E would each have the extension of a future (para-) segment and would eventually coincide with either an even (E) or an odd (O) numbered (para-) segment. Each O and E state would be subdivided into an A and a P region. The signal to form a border would be an O/E but not an A/P confrontation. Although a double segment pattern exists in Drosophila, the segment borders are determined by the segment polarity genes, not by the pair rule genes.
(ii) Segmentation results from the periodic alternation of (at least) three cell states, for instance S, A and P. A segment border would be formed whenever P and S cells are juxtaposed (...P/SAP/SAP/S...). A cyclic sequence of (at least) three cell states has necessarily a polarity since each cell state has anteriorly a different neighbor than posteriorly.
If one of such three cell states were lost by a mutation, the polarity but not the periodicity would be lost. The mutation patch above right provides an example (for further details in the modelling, see Meinhardt 1986a [PDF] ).
Moreover, the separation of each A/P by at least one cell type that is neither A nor P (called here S) provides the precondition that only one A/P confrontation exists per segment. This makes sure that only one leg pair is formed and that these legs have the correct polarity in relation to the AP body axis.
The ordered initiation of segments require additional cues: On its own, stripes generated in this way would have any orientation. Therefore, additional mechanisms are required to orient the segmental pattern and to assure a regular spacing. One possibility is that a posterior growth zone exists. For instance, if sufficient cells of one cell type are present at the growth zone, the activation of the alternative cell state becomes very strong. Since the distance to the cells of the alternative state becomes larger and larger, their stabilizing influence becomes lower and lower until a switch to the other cell state occurs. The result is a regular alternation of cell states:
Such an addition of segments is typical for short germ insects [6].
The addition of new segments at a posterior growth zone is a time-consuming process. A very rapid and simultaneous segment formation is possible by a hierachical nesting of pattern-forming reactions. This is realized in Drosophila.
Generation of a fine structure within a segment: As mentioned, to obtain a polarity a repetition of at least three cell states is required. The final pattern is, however, certainly finer. In Drosophila and many other segmented animals, four cells act as founders for a segment []. So far it is unknown of how the higher spatial resolution becomes is achieved.
A system of locally exclusive but mutually activating cell states has interesting properties if several feedback loops are involved. It displays regulatory features as described above. In simulation given below, a sequence of gene activities emerges. Starting with, e.g., two elements, new structures become induced during marginal growth whenever a the last formed structure is large enough. No overall morphogenetic gradient is required (Meinhardt and Gierer, 1980 ).
The resulting sequences of gene activation are self-regulating. A gap in the sequence is repaired by the intercalation of the missing elements. If surplus structures are present (see Bohn's cockroach experiment above), this is accompanied by a polarity reversal.
The mutual long ranging activation of cell states that locally exclude each other is in its core an alternative version of the local autocatalysis - lateral inhibition scheme . In this case, the inhibition works by a long ranging activation of a competing cell state (Gierer, 1981a) [PDF].
In simulations of experiments in which polarity reversal occurs it it turned out to be a problem that at the point of polarity reversal a particular structure has only one of its usual neighbors. For instance, the structure 4 in the sequence 12345678765456789 mentioned above has not its normal neighbor 3. This imposes constraints about the possible molecular interactions. The model equations have to take into account that a supporting influence of structure 3 on structure 4 is obviously not absolutely required.
Further Reading and References
More details and equations can be found in the book "Models of biological pattern formation", chapter 12 and13 [PDF]
H.M. (1986a). Hierarchical inductions of cell states: a model for segmentation in Drosophila J. Cell Sci. Suppl. 4,357-381 [PDF]
- Locke, M. (1959). The cuticular pattern in an insect, Rhodnius prolixus Stal. J. exp. Biol. 36, 459-477.
- Lawrence, PA (1970). Polarity and patterns in the postembryonic development of insects.Adv. Insect Physiol. 7, 197-266
- Bohn, H. (1970). Interkalare Regeneration und segmentale Gradienten bei den Extremitäten von Leucophaea-Larven. Wilhelm Roux' Arch 165, 303-341.
- von Dassow, G., Meir, E., Munro, E.M. and Odell, G.M. (2000). The segment polarity network is a robust development module. Nature 406, 188-192.
- Ingham, P.W. (1991). Segment polarity genes and cell patterning within the Drosophila body segment. Curr. Op. Gen and Dev. 1, 261-267
- Patel, N. H. (1994). Developmental evolution - insights from studies of insect segmentation Science 266, 581-590



