Initiation of legs and wings: differentiation borders obtain organizing properties

Of course, the structure of a higher organism is more complex than can be achieved by the interpretation two orthogonal gradients. The generation of sub-structures like legs, wings or eyes, requires patterning of secondary fields. These fields must be initiated at precise position and the resulting patterns must obtain the correct orientation with the established axes of the embryo.

The notion of how secondary embryonic fields become established during development where highly influenced by the field concept of Harrison [6]. Based on his experiments with amphibian limbs he proposed that first cells are set aside that will form the future the limb. At later stages an anteroposterior and subsequently a dorsoventral axis becomes determined in these cells.

This model leads to several predictions that are incompatible with the observations (see below). As an alternative I have proposed a different mechanism: secondary fields formed around the intersection of two determination borders. This mechanism is at work in insects [PDF] and in vertebrates [PDF] (Meinhardt, 1983 a,b). Imagine first two adjacent regions with the cell types A and P. Both are assumed to cooperate to produce a new morphogenetic substance. For instance, in the P region could produce a co-factor while the synthesis of the final morphogen m is possible only in the A-region. Thus, the morphogen production is necessarily restricted to the common border.

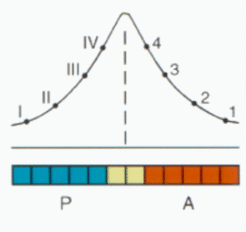
The concentration of the signal in the field is measure for the distance of a cell from the border and is therefore convenient for the internal organization of the A and the P region. Although the positional information is essentially symmetric, the resulting pattern can be asymmetric if A and P cells respond differently. In the extreme case (as in vertebrates, see below), only one type may respond at all.

A border that separates two cell types along the anteroposterior axis surrounds an embryo in a belt-like fashion. To determine the position of a limb along this line the cooperation of another pair of cell types is required. This leads to secondary fields around the intersection of two borders.

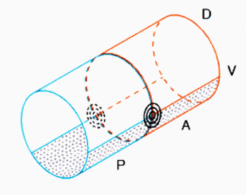
As demonstrated in the figure above, for any reasonable subdivision of an in first approximation cylindrical embryo along the anteroposterior and the dorsoventral axis these intersections occur in pairs, one at the right and one at the left side of the embryo. Both have opposite handedness, a feature of obvious importance for the formation of legs, wings, eyes etc. In other words, the handedness of, e.g., a left limb depends on the topology of the intersection that leads to limb formation, not per se because the structure arises on the left side. As shown further below, a simple shift of tissue can lead to a reversal of the handednes.

In vertebrates, only the anterior tissue responds. The PA/DV border would correspond to the Zone of Polarizing Activity, ZPA. The digits appear in the plane determined by the DV-border.

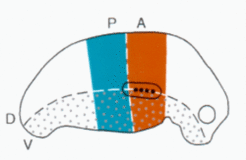
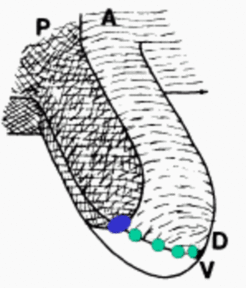
However, the model solves several problems left open in the ZPA model. A local high concentration would lead to a cone-shaped morphogen distribution and a circular structure would be expected (as given in insect limbs). However, the digits are arranged in a plane. In the model proposed, this is because only cells on the DV border can make digits and this only in the anterior tissue.

The model has found direct support from many molecular genetic observations [2-5]. One prediction was that the formation of the border precedes formation of secondary fields. In Drosophila, for instance, the A-P border forms already during segmentation with the specification of the anterior and posterior compartment by the en and wg activation. This is in contrast to Harrison's assumption that a limb field is formed first and obtains subsequently its AP subdivision.

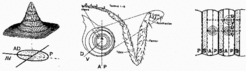
In the Drosophila leg, the confrontation of three sectors was assumed to define the coordinate system. The resulting cone-shaped morphogen distributionaccounts for the concentric fate map of the leg. The three sectors provides a crude circumferential subdivision and thus the handednes of the leg. Assuming an at least threefold subdivision of a segment, the model accounts for the formation of only one leg pair per segment (top right).

These models have found support by molecular-genetic observations. Since these have been reviewed recently [3,11], some classical observations with insect and vertebrate appendages from pre-molecular times will discussed below that illustrates the explanatory power of the model:

(I) AN A-TO-P FLIP CAN LEAD TO NEW INTERSECTIONS AND THUS TO SUPERNUMERARY LEGS

There are temperature sensitive mutants in Drosophila that have the tendency to form leg duplications or triplications. Three legs are always formed in a plane; the two outer legs have the handedness as expected while the central leg has a reversed polarity [1].

As mentioned, segmentation was proposed to be bases on mutually stabilizing cell states. If this stabilization is weakened, a flip from one state into another can occur. This can lead to two new intersections and thus, together with the original one, to three legs. As shown in the figure, the model describes correctly the arrangement in a plane and the handedness of the legs. Meanwhile, supernumerary wings have been formed also by genetically triggered P-to-A transformations [9].

(II) A new A/P juxtaposition can generate a supernumerary leg

As mentioned in connection with segmentation, a repetition of at least three cell states is required to obtain a periodic pattern with an internal polarity. That means, one pair of A/P compartments is separated by at least one state called S ('Separation') that is neither A nor P. Since an A/P confrontation is decisive for the generation of a leg, the removal of the S region would lead to a new P/A confrontation. A corresponding experiment has been done by Horst Bohn [9]. In cockroaches he observed the formation of a supernumerary leg after removal of a part of a metathoracic segment that would never form a segment:

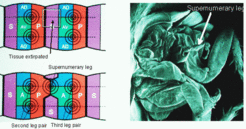
In terms of the model, the operation leads to the removal of the S-region. After wound healing a juxtaposition of the P region of the mesothoracic and the A-region of the metathoracic segment results. In other word, a new border is becomes established that has the opposite polarity, P/A instead of A/P. Since the DV level is unchanged, the condition for leg formation is fulfilled. As expected from the model, the result is an AP-reversed supernumerary leg. Since the DV axis remains unchanged, the leg has the opposite handedness.

(III) Vertebrate limbs: shift of tissue along the AP axis can lead to polarity reversal.

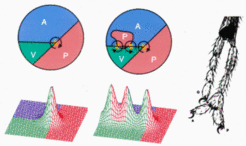
Harrison was convinced that the polarity of the embryonic AP axis imposes the polarity of the limb. Therefore, it was most puzzling for him [7 ] that transplantations of small pieces of tissue can either lead to symmetric limbs or to limbs with a reversed polarity. The figure below illustrates that the model provides a coherent explanation for the observations of Harrison [6,7] and Slack [8]. Top: normal situation. By cooperation a symmetrical morphogen distribution results. Only the A region can respond. The single exponential gradient in the A region (red curve) determines the sequence of the digits (high = little finger). Centre: A P-region is transplanted in front of an A region. A symmetrical P-A-P pattern, a symmetrical positional information (red curve) and thus a symmetrical limb with posterior digits at each end is formed. Bottom: The reverse experiment: A cells are transplanted to a more posterior position. Although the pattern is again symmetric (A-P-A), two exponential gradients (red curves) and thus two limbs result. The posterior arm has a reversed polarity. This observation was very puzzling for Harrison since he assumed that the overall polarity of the body axis orient the AP axis of the limb. Even more striking, since the operation does not change the dorsoventral pattern, if the operation is performed at the right side, the supernumerary limb will have the symmetry of a left limb.

Initiation of legs and wings: differentiation borders obtain organizing properties

Further Reading and References