Relation to Turings's mechanism
In 1952, Turing [1] discovered that spatial concentration patterns can be generated by auto- and cross-catalytic interactions of two substances with different diffusion rates. His mathematical demonstration was based on a Fourier analysis of instabilities of uniform distributions. He exemplified the mechanism envisaged by the following set of equations (Turing, 1952, p.42 [PDF] ).
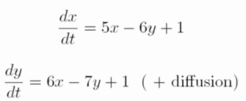
Turings example
His paper did not mention any requirements of long range inhibitory effects. Both equations look very similar and it is not immediately obvious why such an interaction allows pattern formation. What, then, is the relation to our concept of lateral inhibition? In retrospect, it is not difficult to see that this interaction does satisfy our condition of local autocatalysis (of x ) and the long range inhibition via a molecule (y) whose production is under x- control and that acts antagonistically, in this case, by destruction the x molecules. Therefore, Turing's mechanism can generate basically the same types of patterns as do models primarily and explicitly based on autocatalysis and lateral inhibition, i.e., graded concentration profiles and one or several isolated maxima. However, knowing that the crucial condition is local self-enhancement that is balanced by a long-ranging inhibitory reaction facilitates substantially the design of appropriate reactions.
The mechanism proposed by Turing`s equations given above have an essential drawback in that they are not reasonable in molecular terms: The number of x molecules disappearing per time unit is assumed to be proportional to the number of y molecules but independent of the number of x molecules. In other words, x molecules can disappear although no x molecules are present. This can lead to negative concentrations. Turing has seen this problem and proposed to ignore negative concentrations, and beyond this he realized the requirement for non-linear interactions.
Although Turing did not refer to mechanisms corresponding to lateral inhibition in his paper, in unpublished notes found after his death there are sentences alluding to inhibitory processes: "The amplitude of the waves is largely controlled by the concentration V of 'poison'..... " [2].
Further Reading and References
A detailed analysis of the relation of concepts based on Fourier wave methods (as introduced by Turing) and our mechanisms based on autocatalysis and long-range inhibition can be found in the following two papers:
Gierer, A. (1981) Generation of biological patterns and form: Some physical, mathematical, and logical aspects. Progr. Biophys. molec. Biol. 37, 1-47 [ PDF ].
Gierer, A (1988). Biological Pattern Formation and Physico-Chemical Laws. In: Synergetic and Dynamic Instabilities [ PDF ]
- Turing, A. (1952). The chemical basis of morphogenesis. Phil. Trans. B. 237, 37-72 [available from the web]
- Hodges, A. (1983) Alan Turing: the enigma. Simon and Schuster, New York; quotation is on page 494.
[Back: Primary Pattern Formation]
[Back: Index]
